更新时间:2022-07-05 来源:黑马程序员 浏览量:
数字类型不仅可以参与简单的加减乘除等基本运算,还可以参与更加复杂的数学运算,比如求弦、求根、求对数等,在Python程序中实现这些运算需要用到Python的一个数学模块——math。在使用math模块之前,需要先用import语句导入math模块:
import math
math模块提供了几个数学常量和众多数学函数,接下来将带领大家从这两方面认识一下math模块。
在众多数字运算中都会用到一些特别的常数,例如,圆周率m、自然对数的底e等。math模块提供了4个常数:pi、e、inf、nan,它们对应的数学符号和表示的含义如表1所示。
表1math常数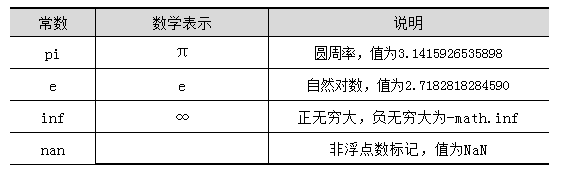
下面利用math模块来输出圆周率m和自然常数e的值(精确到小数点后20位):
# 03_calculation.py
import math
print("圆周率π:%.20f"% math.pi) #精确到小数点后20位
print("自然常数e: %.20f" %math.e) #精确到小数点后20位数学中除了基本的运算以外,还支持一些特殊运算,比如求绝对值、阶乘,最大公约数等。ma山模块提供了一些数值表示函数。这些涵数的数学符号和功能描述如表所示。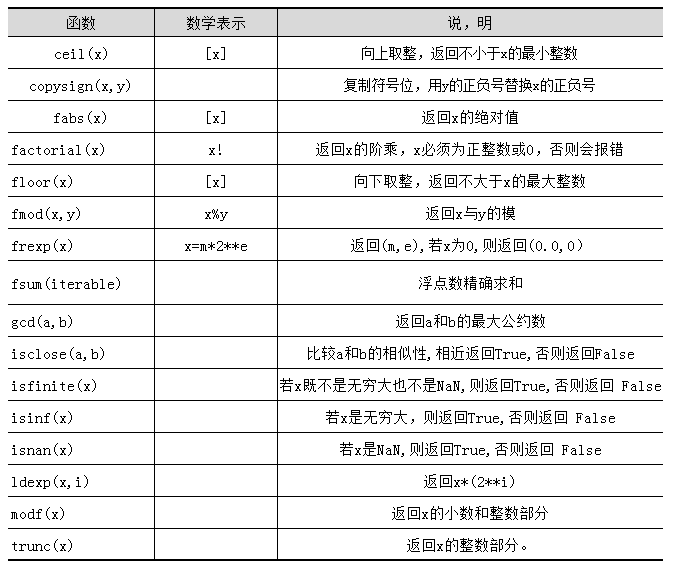
Python中浮点数的精度有限,无法支持高精度浮点数的运算。为了解决这个问题,math库提供了一个计算多个浮点数和的函数math.fsum(iterable)。这个函数不仅高效,还可以减少因计算导致的误差。
数学中10个0.1相加的结果为1.0,下面分别用Python中的运算符和math模块中的fsum()函数进行计算,代码如下:
>>> 0.1+0.1+0.1+0.1+0.1+0.1+0.1+0.1+0.1+0.1 0.9999999999999999 >>> math.fsum([0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1]) 1.0
由上述示例结果可知,直接使用运算符计算的结果不是1.0,而使用fsum()函数计算的结果为1.0。产生这种情况,主要是因为Python中表示0.1时小数点后存在若干位的精度尾数,在0.1参与加法运算时,这个精度尾数可能会影响输出结果。因此,在涉及到浮点数运算和结果比较时,建议使用math模块中提供的函数。
数学中的幂运算和指数运算是比较常见的,math模块针对这些运算提供了相应的函数,关于这些函数所对应的数学符号和功能说明如表3所示。
表3幂函数和对数函数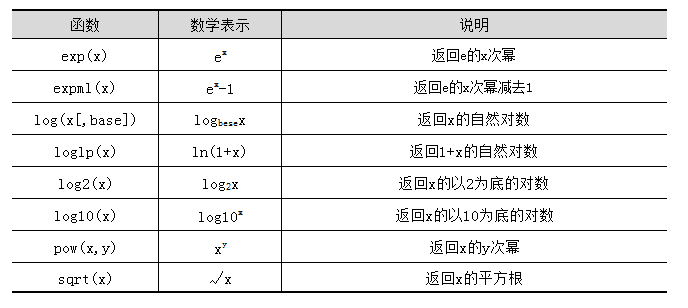
在指数运算中,如果调用pow()函数时传入的指数小于1,则表示该函数做的是开根运算。例如,对27执行开立方根运算:
>>> math.pow(27, 1/3) #返回27的立方根 3.0
三角函数将三角形中的角与其边长相互关联。在标准库中,所有的三角函数的输入都是弧度。math模块中三角函数的数学表示与功能说明如表4所示。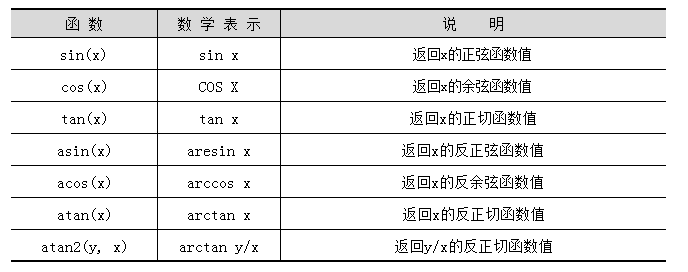
除此之外,mA山模块中还增加了一些具有特殊功能的函数,关于它们的功能说明如表所示。

高斯误差函数在概率论、统计学以及偏微分方程中有着广泛的应用,而伽玛函数在分析学、概率论、偏微分方程和组合数学中有着广泛的应用,它们均不属于初等数学,但是非常有趣。例如,利用伽玛函数计算浮点数的“阶乘”,代码如下:
>>> math.gamma (6) +求0~5范围内的整数阶乘 120.0